Gestalterisch sind Ellipsen eine schöne geometrische Form. Sie wirken beispielsweise bei Tischplatten sehr gut. Bei Ellipsen handelt es sich um spezielle Ovale. Da diese durch zwei unterschiedlich lange, sogenannte Halbachsen, eindeutig definiert werden, lassen sie sich sehr exakt konstruieren und auch fräsen. Das geht sogar erstaunlich einfach. Wenn beide Halbachsen gleich lang sind bekommt man anstatt einer Elses einen Kreis.
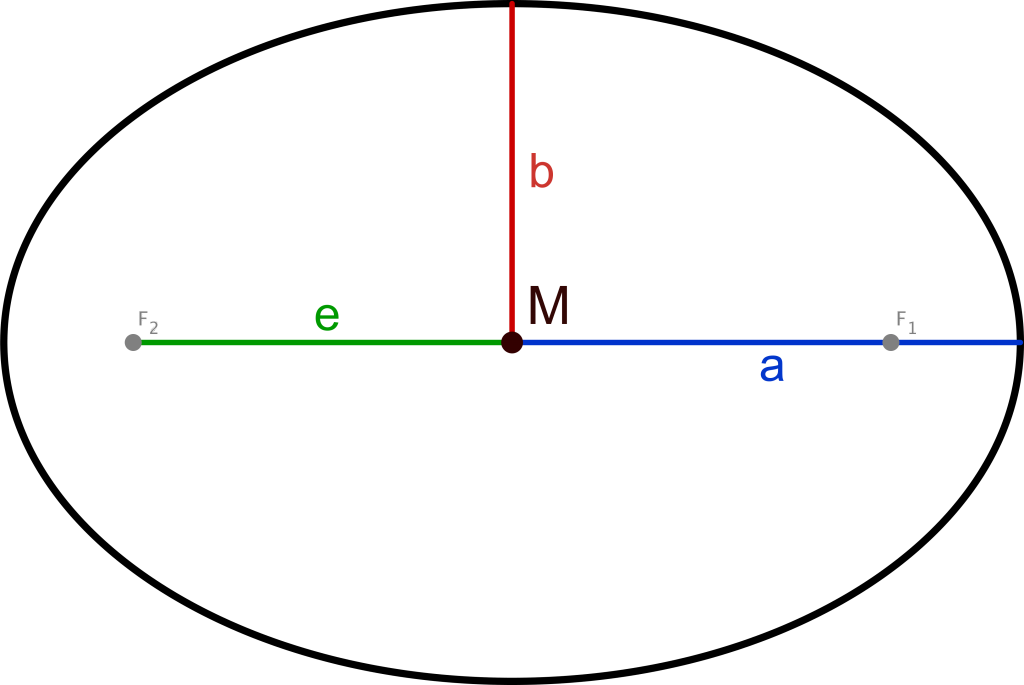
Auf der Zeichnung ist eine Ellipse mit den wichtigsten Merkmalen zu sehen. Der Mittelpunkt sollte selbsterklärend sein. Die beiden Strecken a und b stellen die Halbachsen dar. Die Strecke e repräsentiert den Abstand vom Mittelpunkt zu den beiden Brennpunkten. Diese werden Teilweise als Hilfs Punkt zum konstruieren benötigt.
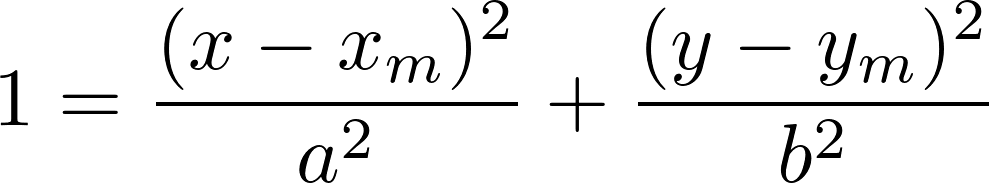
Die Gleichung der Ellipse sieht auf den ersten blick komplizierter aus wie sie es ist. Vereinfachen lässt sich die Gleichung in dem der Mittelpunkt der Ellipse auf den Koordinatenursprung gelegt wird.
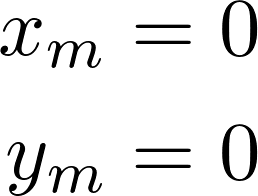
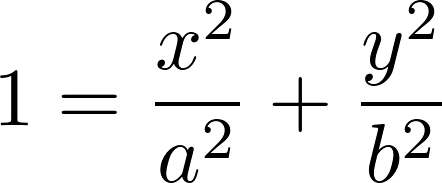
Um die Strecke e (Abstand der Brennpunkte vom Mittelpunkt) berechnen zu könne muss zunächst folgendes definiert werden:
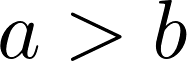
Wäre b > a würde die Formel zur Berechnung von e kein reelles Ergebnis liefern.
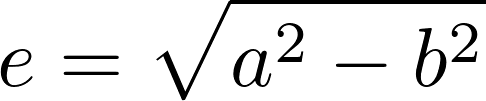
Die Berechnung des Flächeninhalts einer Ellipse ist sehr einfach. Auch an dieser Formel lässt sich die Verwandtschaft zum Kreis nicht leugnen.
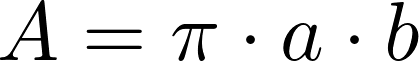
Um die länge eines eventualen Umleimers zu berechnen wäre es von Interesse den Umfang einer Ellipse zu bestimmen. Dies ist leider deutlich schwieriger wie der Flächeninhalt. Auf umfangreiche Integrale möchte ich an dieser stelle verzichten. Oft sollte eine Überschlagsmäßige Berechnung ausreichend sein. Die folgende Formel ist hierbei hilfreich:
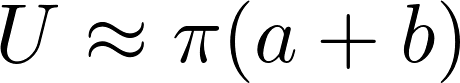
Achtung die Formel ist eine grobe Näherung. Nur wenn a und b gleich sind (eigentlich ein kreis und keine Ellipse) liefert die Formel exakte Werte. Umso grösser die Differenz zwischen a und b wird umso stärke weicht das Ergebnis vom tatsächlichem Wert ab. Hierbei sind Abweichungen von über 20% möglich.
In diesem Beitrag möchte ich zwei Methoden vorstellen wie sich Ellipsen mit einfachen mitteln konstruieren lassen. Beide Methoden habe ich verwendet um eine Ellipse mit den Abmaßen:
Halbachsen:
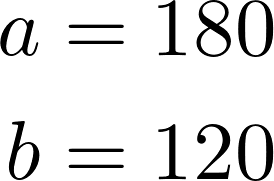
Um die tatsächliche Größe der Ellipse zu bestimmen werden die Werte der Halbachsen verdoppelt.
Zu Zeichnen.
Gärtner Methode
Hierfür werden lediglich eine Schnur und zwei Drehpunkte (Nägel oder Schrauben) benötigt. Die Drehpunkte liegen auf den beiden Brennpunkten der Ellipse. Um deren Position zu bestimmen muss zunächst der Wert e berechnet werden.
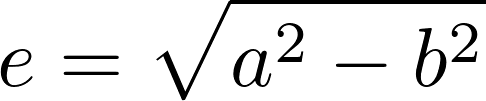
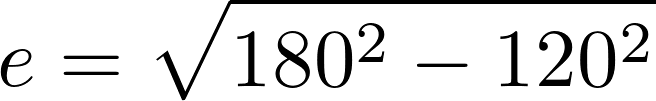
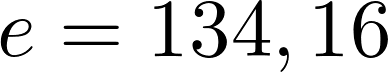
Auf einer Geraden lässt sich der Mittelpunkt der Ellipse festlegen. Die Beiden Brennpunkte werden mit dem ermitteltem abstand e = 134,16mm vom Mittelpunkt aus abgetragen.
Als nächstes wird die Schnur zu einer Schlaufe geknotet. Die Größe der Schlaufe ist entscheidend dafür wie Groß die Ellipse werden soll. Die länge der Schnur für die Schlaufe lässt sich wie folgt ermitteln:
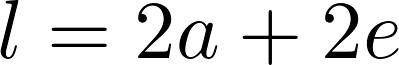
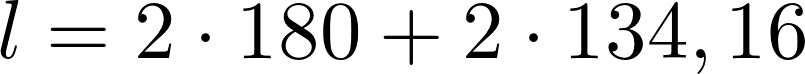
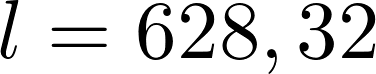
Die Schlaufe wir über die zwei Drehpunkte gelegt und mit einem Stift gespant. Wird der Stift einmal rundum bewegt erhält man eine Ellipse. Wichtig ist es hierbei darauf zu achten das die Schnur immer gespannt bleibt.


Ellipsenzirkel (Ellipsograph des Archimedes)
Bei der zweiten vorgestellten Methode wird der Stift zwangsgeführt. Der Stift des Zirkels lässt sich gegen eine Oberfräse austauschen und es kann direkt eine Ellipse gefräst werden ohne sie vorher anzeichnen zu müssen.
Das Kernstück des Zirkels bildet ein, mit überkreuz angeordneten führungsnuten, Grundplatte. In jeder der Zwei Nuten befindet sich ein Kulissensteine mit Bohrung. Der Arm des Zirkels ist mit Bolzen in den Bohrungen der Kulissensteine gelagert. Um Ellipsen verschiedener Größen fertigen zu können bietet es sich an den Arm mit mehreren Bohrungen zu versehen.
Den Zirkel gibt es als Einsatzbereite Einheit zu kaufen. Ihn selbst zu bauen ist jedoch nicht schwierig und hinsichtlich der benötigten Größe hat man freies Spiel.
Beim „Einstellen“ des Zirkels sind die Abstände von der Position wo Gezeichnet/Gefräst wird hin zu den Bohrungen ausschlaggebend. Es wird jeweils eine Bohrung im Abstand a und eine im Abstand b benötigt.
Die Grundplatte wird auf den späteren Mittelpunkt ausgerichtet und Fixiert. Der arm des Zirkels lässt sich drehen und dank der Zwangsführung entsteht eine Ellipse.




