Für den Bau eines runden Tisches stand ich vor der Herausforderung einen hölzernen Kreisring zu fertigen. In diesem Beitrag beschreibe ich meine Herangehensweise den Kreisring aus einem regelmäßigem Polygon zu erhalten. Den bau des Tisches stelle ich in einem separatem Beitrag vor.
Inhaltsverzeichnis:
- Schrittweise Vorgehensweise
- Auswahl eines geeigneten Polygons
- Excel zum Berechnen der Trapeze
- Berechnung der Größe der Trapeze
Schrittweise Vorgehensweise
Mein vorgehen bei der Herstellung des Kreisrings habe ich in die folgenden Schritte Gegliedert:
- Ziel mit Innen und Außen Durchmesser festlegen
- Ermitteln der Größe der Trapeze für den Rahmen
- Verleimen des Polygon förmigen Rahmen
- Mit einem Fräszirkel die äußeren Ecken Abrunden
- Den inneren Kreis fräsen (kann übersprungen werden)
- Fertiges Ergebnis des Kreisrings
Zur Verdeutlichung der einzelnen Schritte eine Grafik:
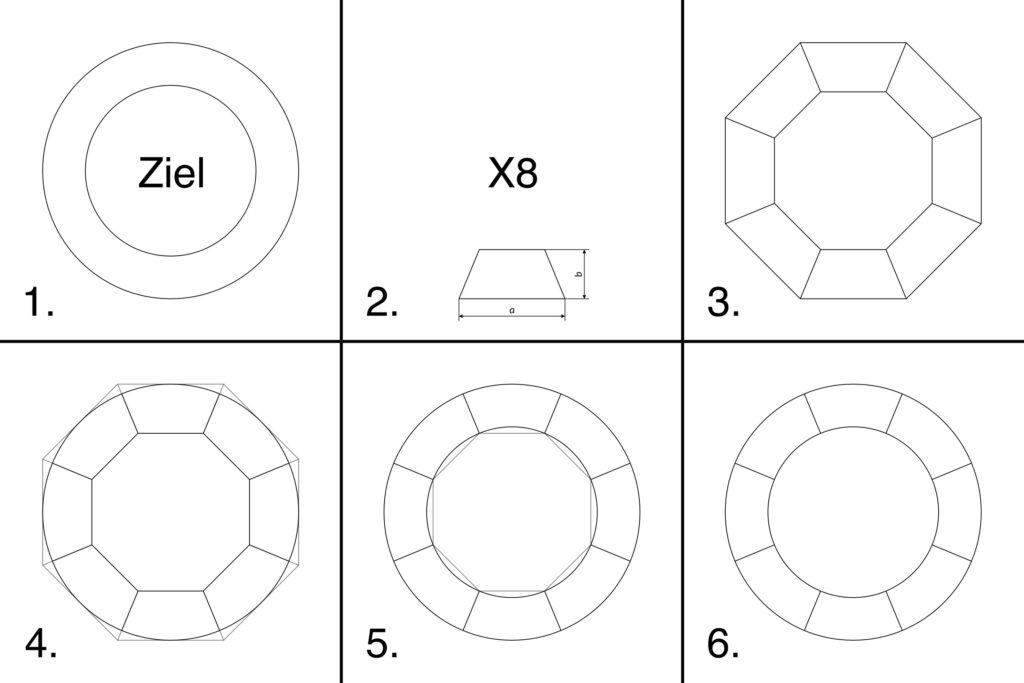
Auswahl eines geeigneten Polygons
Bevor ich wirklich loslegen konnte galt es ein geeignetes Polygon auszuwählen. Desto mehr Ecken das Polygon hat desto weniger verschnitt fällt beim späteren fräsen an. Theoretisch Gäb es keinen Verschnitt, wenn das Polygon unendlich viele Ecken hätte. Praktisch ist dies natürlich nicht möglich. Zumal auch unendliche Verluste bei der Herstellung der unendlich vielen Rahmenteile anfallen würden.
Wie viel Verschnitt tatsächlich anfällt hängt von dem Verhältnis von innen und außen Durchmesser ab. Alle weiteren Betrachtungen beziehen sich auf einen Kreisring mit folgenden Abmessungen: äußerer Durchmesser D=600mm und einem innerer Durchmesser d=400mm.
Bei einem Rahmen in form eines Dreiecks ist der Verschnitt sehr hoch. Weggefräst werden rund 62 Prozent. Um dies zu veranschaulichen folgend eine Grafik. Die grün eingefärbten Bereiche sind die letztendlich benötigten. Die rot eingefärbten Bereiche werden weggefräst und somit entsorgt.
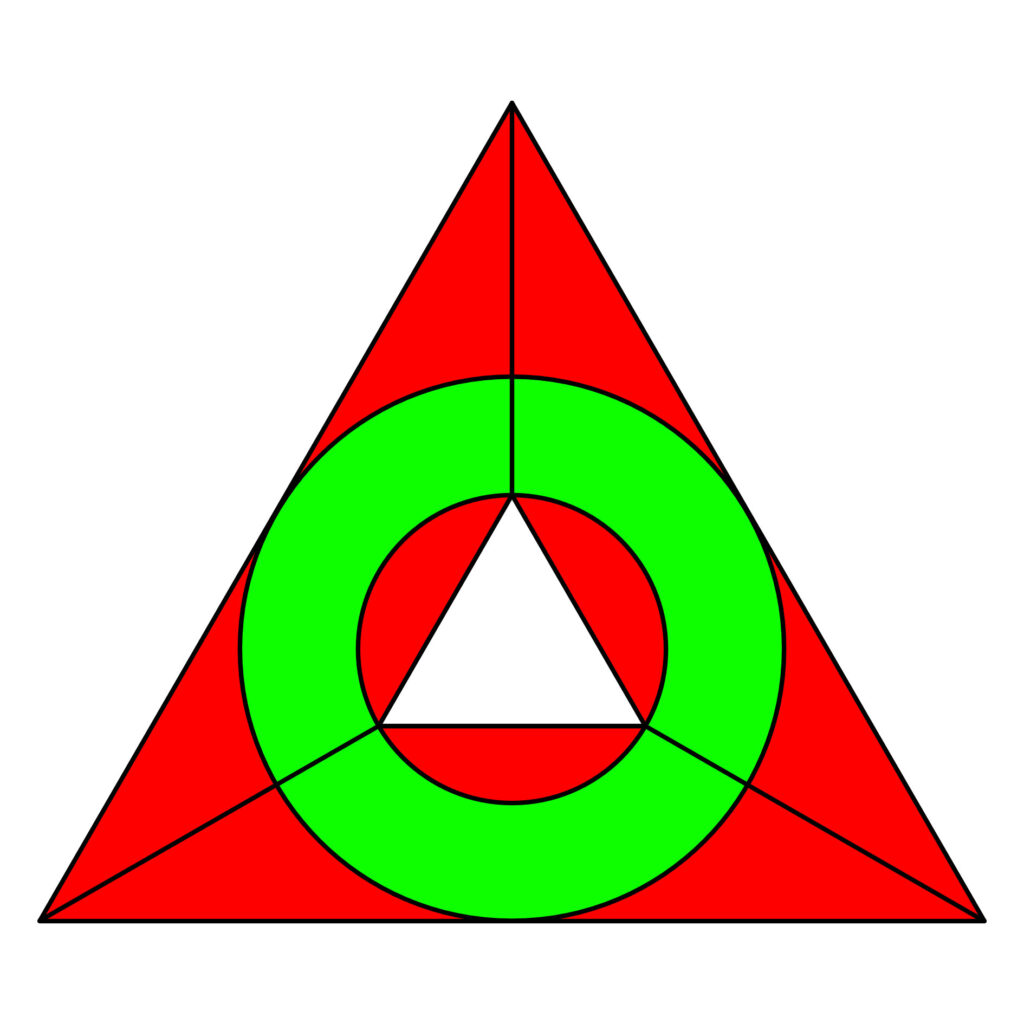
Ich habe mich für ein Oktagon entschieden. Hier ist der Verschnitt mit rund 15 Prozent deutlich kleiner. Optisch lässt sich gleich erkennen, dass die roten Bereiche deutlich weniger Dominat sind.
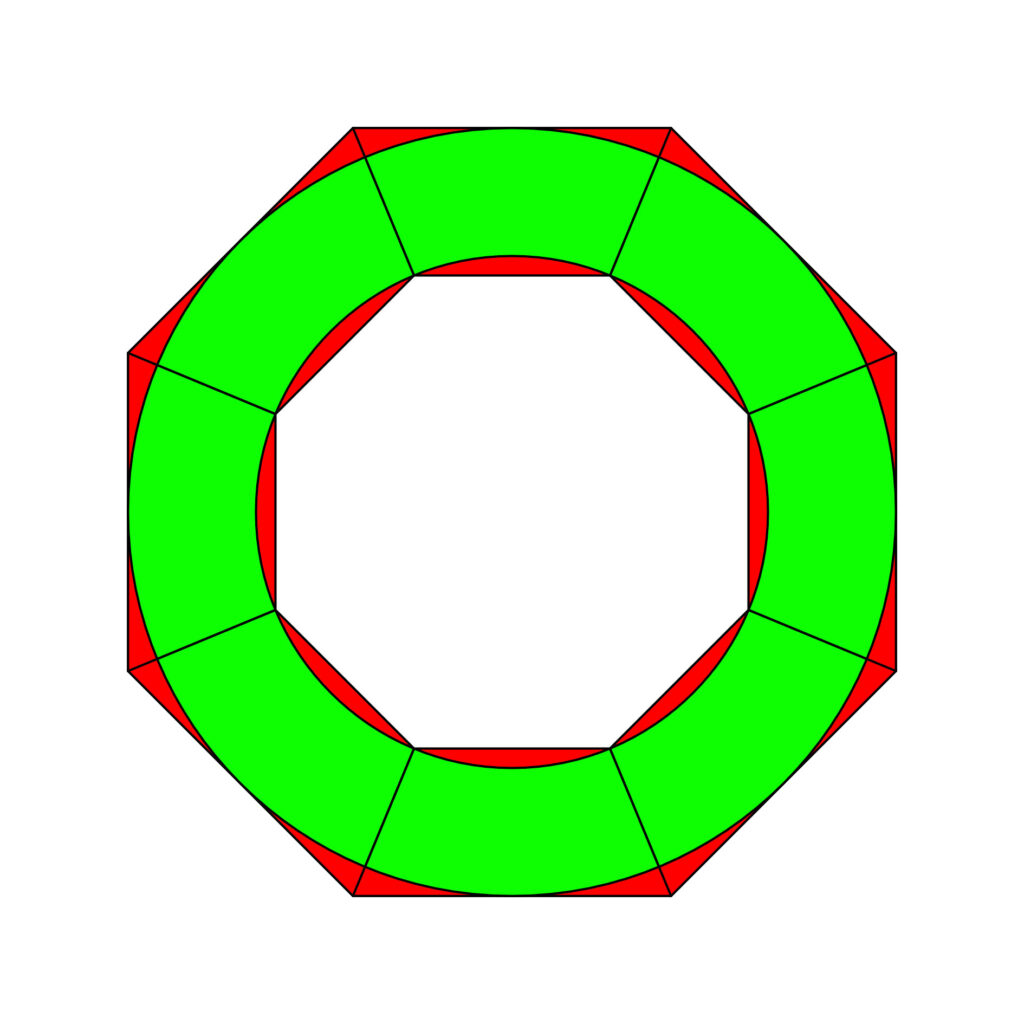
In einer kleinen Tabelle habe ich die prozentualen Verluste verschiedener Polygone gegenübergestellt.
| Bezeichnung | Anzahl Ecken | Verschnitt in Prozent |
| Trigon | 3 | 62% |
| Tetragon | 4 | 44% |
| Pentagon | 5 | 32% |
| Hexagon | 6 | 24% |
| Oktogon | 8 | 15% |
| Dekagon | 10 | 10% |
| Dodekagon | 12 | 7% |
Excel zum Berechnen der Trapeze
Wer möglichst schnell wissen will welche Abmaße die Trapeze für den Rahmen brauchen kann dies mithilfe des folgenden Excel Dokuments ermitteln. Einzutragend sind lediglich der innere und äußere Durchmesser des gewünschten Kreisrings. Ausgegeben werden alle Abmaße des Trapezes. Sicherlich ist es vernünftig zu den theoretisch genauen Maßen etwas Aufmaß dazuzugeben.
Auf einem weiteren Tabellenblatt lassen sich die anfallenden Verschnitte von verschiedenen Polygonen vergleichen.
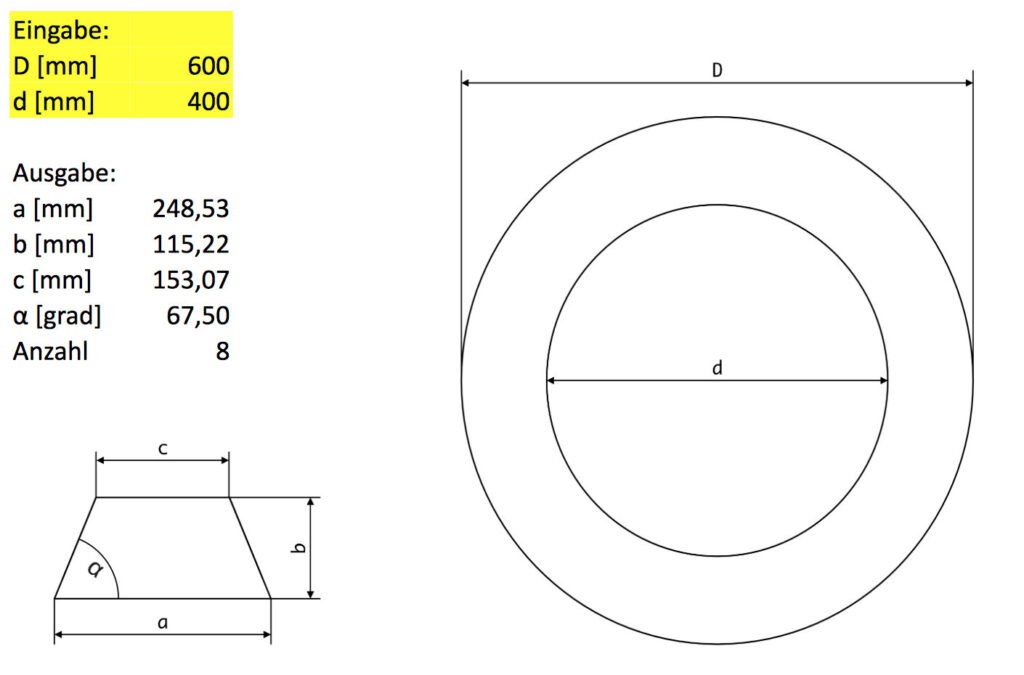
Berechnung der Größe der Trapeze
Viel schöner ist es selbst zu berechnen in welcher Größe die Trapeze anzufertigen sind. Eine gute Gelegenheit etwas Mathematik anzuwenden. Mir hat es definitiv Spaß gemacht. Viel vergnügen mit den folgenden Formeln.
Die Zwei Wichtigsten Formeln sind die des Innen- und Umkreises eines Achtecks. Bei anderen Polygonen ist das vorgehen gleich lediglich werden entsprechend andere Formeln benötigt. Paradoxer weise wird der Innenkreis für den äußeren Durchmesser der Kreisrings benötigt. Für den inneren Durchmesser ist die Umkreisformel anzuwenden.
Der Innenkreis von einem Achteck:
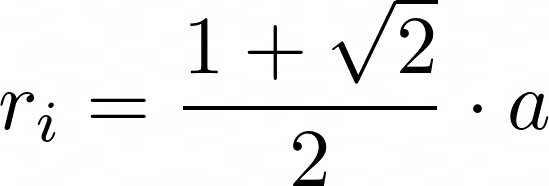
Der Umkreis von einem Achteck:
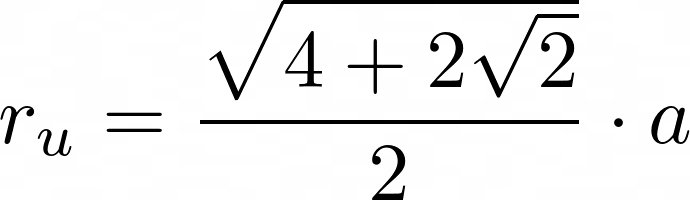
Beide Formeln habe ich anschließend nach a aufgelöst.
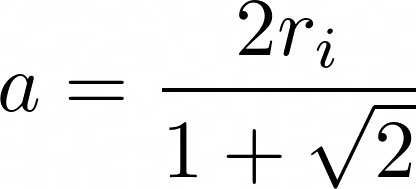
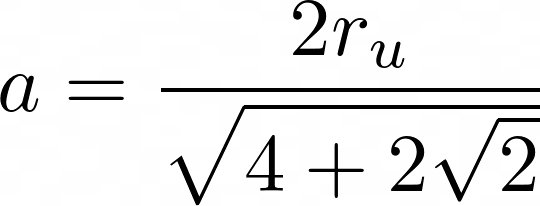
Weiter ging es mit der Trigonometrie. Zunächst habe ich die Trapeze in ein Rechteck und zwei gleiche Dreiecke aufgeteilt. Von den Rechtwinkligen Dreiecken waren mir alle Winkel bekannt. Die unten an dem Rechten Winkel anliegende Seite ist genau halb so lange wie die Differenz von a. Mithilfe dieser Angaben lies sich die Höhe der Trapeze mit dem Tangens einfach bestimmen.
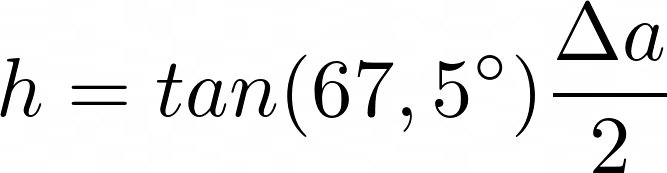
Zur Verdeutlichung noch eine beschriftete Zeichnung des Trapezes:
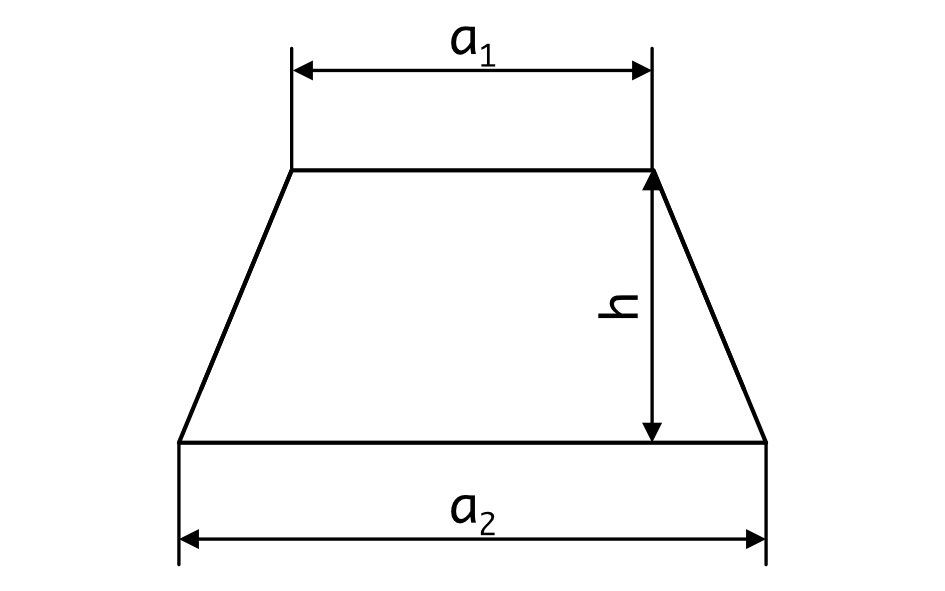
Abschließend die oben genannten Formeln mit eingesetzten Zahlen. Angewandt habe ich die Formeln, wie auch schon weiter oben, für einen Kreisring mit folgenden Abmessungen: äußerer Durchmesser D=600mm und einem innerer Durchmesser d=400mm.
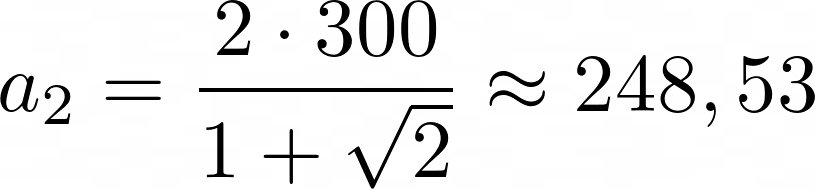
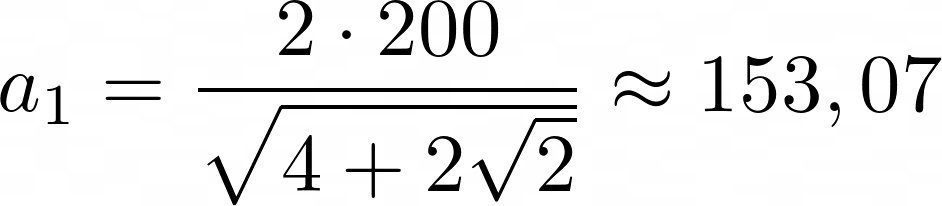
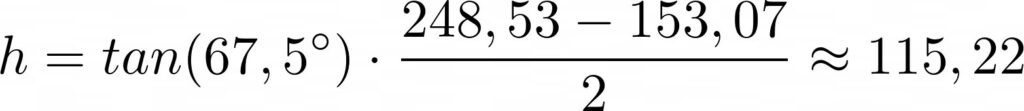
Im nächsten Monat zeige ich die Anwendung des ganzen beim bau eines kleinen Gartentisches.


